目次
はじめに:命題論理について
大学の研究室に所属されている方の多くは、先生から「ロジカルシンキングで物事を考えろ」と言われた経験があるのではないでしょうか。
なるほど確かに、論理的に物事を考えるのは学術研究では必須の能力と言えるでしょう。
しかし、ここで言われている「論理的」とは、一体何を指すのでしょうか。
「論理的であるとは…………論理的であることだ」
と、小泉進次郎氏のような答えしか頭に浮かんでこない方も多いのではないでしょうか(私は実際そうでした)。
そこでこの記事では、論理を厳密に論理的に問い直す学問「論理学」の基礎となる「命題論理」についてご紹介します。
論理学の世界は本当に奥深く、この記事ではその入口しかお見せできませんが、この記事が皆様の論理への知的好奇心を満たす内容になっていれば幸いです。
(注釈:この記事で取り扱うのは、アリストテレスが創始した「名辞論理学」ではなく、19世紀後半にラッセル・フレーゲ・ホワイトヘッドらが考案した「記号論理学」です。
名辞論理学と記号論理学の違いについては以下の記事をご参照ください。
https://online-library.site/?p=1283
論理学(命題論理・述語論理)とは
論理学の具体的な内容について語る前に、論理学の概要を簡単に説明しておきましょう。
論理学は、基本的に「命題論理」と「述語論理」に分けられます。命題論理が「原子文」を単位とする論理学なのに対して、述語論理は「原子文」の中身である「個体変数」と「述語」を単位とする論理学です。
……「いきなり何やら難し気な単語が爆誕したぞ」と思われたかもしれませんが、心配はご無用です。単語は堅っ苦しいですが、それほど難しい内容ではありません。
原子文とは、文としてそれ以上切り分けられない文(命題)のことです。ちなみに、切り分ける余地のある文は「複合文」と言います。
例えば、以下の2つの文を読んでみてください。どちらが原子文かわかりますか?
- 明日は新宿で雨が降るだろう。
- 明日新宿で雨が降ったら、私たちは池袋へショッピングに行く予定だ。
1つ目が “Tomorrow it will rain in Shinjuku.” というSV型の1つの文のみで構成されているに対して、2つ目は “If tomorrow it rains in Shinjuku, I’m going to go shopping in Ikebukuro.” なので、文としてはifから始まる従属節とカンマより後の主節に分けられますね。
従って、1つ目の文が原子文、2つ目の文が複合文になります。
「明日は新宿で雨が降るだろう」などの原子文をp, qなどと表して、原子文p,q同士の関係を「かつ」「または」「ならば」などの接続詞で表現して論理を作るのが命題論理です。
これに対して、原子文p,qを更に細かく分割して論理を作るのが述語論理です。
「私はショッピングに行く」という原子文について考えてみましょう。
述語論理において最初に注目されるのは述語です。この場合は「ショッピングに行く」ですね。この述語を「F」とおきます。
次に注目するのは主語(述語論理では「個体変数」と呼ばれます)。この原子文では「私」ですね。この個体変数(主語)を「c」とおきます。
ゆえに、「私はショッピングに行く」という原子文は、述語論理ではFcと表記されることになります。述語Fと個体変数cを基本要素として文を作り、「かつ」「または」「ならば」などの接続詞で文同士を繋いで論理を作るのが述語論理です。
命題論理よりも細かい単位で論理を構築するので、述語論理は命題論理の発展版と考えられますね。
この記事では、あらゆる論理学の基礎となる命題論理を扱います。述語論理については別途記事を用意したいと思っていますので、お楽しみに!
命題論理の構文論
命題論理にせよ述語論理にせよ、論理学は厳格な論理プロセスを経て、論理的に真である命題を見つけ出すことを目的としています。
この目的を達成する手段は2つあります。1つ目が今から紹介する構文論。もう1つが後で紹介する意味論です。
構文論と意味論の違いは、一言で言うと「文そのものの真偽を考慮するかどうか」に尽きます。真偽を考慮するのが意味論で、考慮しないのが構文論です。意味論の「意味」とは、つまり文の真偽のことなのです。
構文論では、文自体の真偽を考慮せずに論理的に真な命題を探究するのですが、そのときに使うのが「証明」になります。
証明の方法はいくつかありますが、ここでは最も有名な推論形式をご紹介します。
- 推論図を立てる
- 推論図と推論規則から定理を導く
- 定理と推論規則から別の定理を導く
- 以下③を繰り返す
キーワードは「推論図」と「推論規則」と「定理」です。中でも「推論図」は全ての証明の基礎になるので、まずはここから説明しましょう。
推論図とは、現代数学の言葉で言うと「公理」に相当する言葉です。要は絶対に疑いようのない真理ということですね。
命題論理における推論図(公理)は、以下の8つです。
- 連言導入則
- p, qならば、pかつqである
- 連言除去則
- pかつqならば、pである
- pかつqならば、qである
- 選言導入則
- pならば、pまたはqである
- qならば、pまたはqである
- 選言除去則
- 以下3つの前提が与えられているとき、rが真である
- pまたはqである
- pであると仮定するとき、rである
- qであると仮定するとき、rである
- 以下3つの前提が与えられているとき、rが真である
- 条件法導入則
- 以下の前提が与えられているとき、pならばqである
- pであると仮定するとき、qである
- 以下の前提が与えられているとき、pならばqである
- 条件法除去則
- 以下の前提が与えられているとき、qである
- pである
- pならばqである
- 以下の前提が与えられているとき、qである
- 否定導入則
- 以下の前提が与えられているとき、pでない
- pであると仮定するとき、qかつ「qでない」
- 以下の前提が与えられているとき、pでない
- 否定除去則
- 『「pでない」でない』ならば、pである
- 【補足】これらの公理に登場する「仮定」は、以下の条件を満たした上で使う。
- 条件①:仮定は、一度解除したら使ってはならない
- 例:条件法導入則を使って、仮定「pである」から結論「pならばqである」を導いた場合、その後の証明で仮定「pである」を使ってはならない
- 条件②:仮定は、解除前ならば何度でも使える
- 例:条件法導入則を使って、仮定「pである」から結論「pならばqである」を導く場合、その導出過程の中である限り仮定「pである」は何度でも使える
- 条件①:仮定は、一度解除したら使ってはならない
連言(かつ)、選言(または)、条件法(ならば)、否定(でない)という4つの論理演算子に対して、「導入則」と「除去則」が与えられています。
「かつ」とか「または」とかは見覚えがあると思いますが、「導入則」「除去則」は馴染みのない単語ですよね。
名前はいかついですが、意味は単純です。シンプルに、
- 前提として使う原子文の数が、推論の結果導かれる原子文の数を下回るタイプの推論規則:導入則
- 前提として使う原子文の数が、推論の結果導かれる原子文の数を上回るタイプの推論規則:除去則
と考えてください。原子文を新たに「導入」するのが導入則で、既存の原子文を「除去」するのが除去則です。
これら、たった8つの推論図から、論理的に可能な全ての推論を導くことができます。後でいくつか代表的な推論をお見せするので、ぜひご期待ください。
命題論理の意味論
続いて意味論の説明に入ります。
初めに意味論と構文論の違いをおさらいしておきましょう。
意味論と構文論の違いは、一言で言うと「文の真偽を考えるかどうか」にあります。真偽という意味を考慮するのが意味論で、考慮しないのが構文論です。
従って、構文論で「pである」と表現されていた命題は、意味論では「pは真である」と表現されるようになります。
意味論でも、構文論と同じように、いくつかの前提を使いながら証明をしていくのですが、その方法は全然違っています。
意味論の証明では、構文論の証明とは違って、以下のような「真理値表」を使って証明していきます。
試しに、いわゆる「三段論法」(「pならばq」かつ「qならばr」、ならば「pならばr」)を意味論的に証明してみましょう。
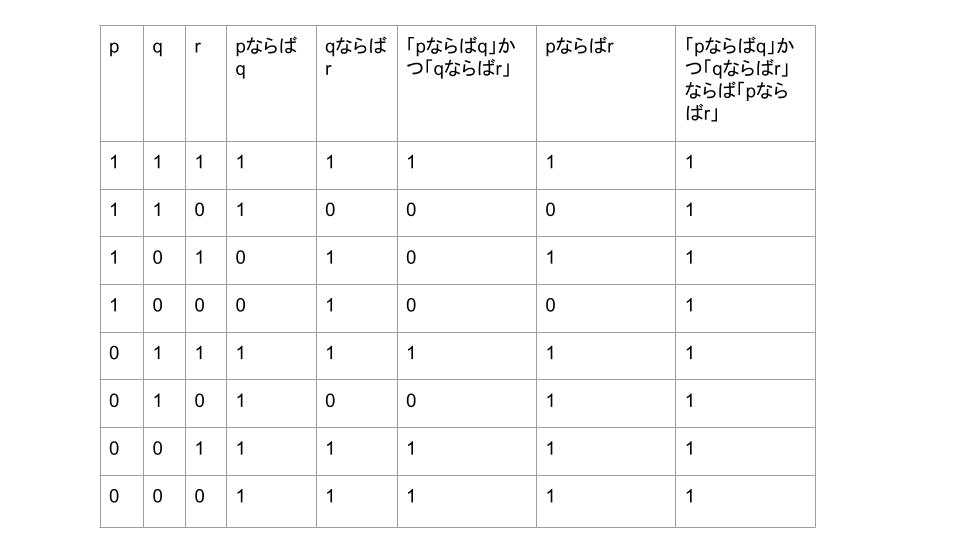
この表の「1」は「真である」を、「0」は「偽である」を意味しています。
表の一番右の列を見てください。
p, q, rが真であっても偽であっても、「pならばq」かつ「qならばr」、ならば「pならばr」が真であることがわかりますよね。
「真である」を意味する「1」と、「偽である」を意味する「0」とを場合わけして調べることで、構文論のような論理のステップを踏まずとも証明を完了させることができています。ずいぶん直感的にわかりやすい証明です。
「じゃあ全部意味論的に証明すればいいじゃん」と思うかもしれませんが、真理値表を使った証明は、登場する命題が複雑になればなるほど煩雑になります(n個の命題が登場する場合、真理値表の行数は2のn乗になります)。
それに何より、真理値表の証明は論理性が見えづらいので、あまり綺麗ではありません。見た目がいかつくても、論理の流れが可視化されている構文論の証明の方が、私は良いと思っています。
というわけで、命題論理に関しては、基本的には構文論で証明しつつ必要があれば意味論によって証明するのがオススメです。ぜひ実践してみてくださいね。
命題論理を使った発展的な証明
命題論理の証明①:「pならばq」と「『pでない』またはq」は同値
ここまで、命題論理の構文論と意味論の違いを説明してきました。
ここからは、構文論と意味論の基礎知識を踏まえながら、汎用性のある定理を2つ構文論的に証明していきます。
1つ目はこちらです。
「pならばq」と「『pでない』またはq」は同値。
「ならば」が「または」に言い換えられるという、なんとも不思議な定義です。
早速証明してみましょう。
「pならばq」ならば「『pでない』またはq」であることを証明
証明に入る前に、「同値」の定義を確認しておきましょう。
一般に、「pとqが同値」とは、「『pならばq』かつ『qならばp』である」ということを指しています。ですから、同値を証明するには「pならばq」と「qならばp」を両方証明する必要があります。
というわけで、まずは
「『pならばq』ならば『「pでない」またはq』」
を証明しましょう。参考までに、命題論理の公理を再掲しておきます。適宜参照してください。
- 連言導入則
- p, qならば、pかつqである
- 連言除去則
- pかつqならば、pである
- pかつqならば、qである
- 選言導入則
- pならば、pまたはqである
- qならば、pまたはqである
- 選言除去則
- 以下3つの前提が与えられているとき、rが真である
- pまたはqである
- pであると仮定するとき、rである
- qであると仮定するとき、rである
- 以下3つの前提が与えられているとき、rが真である
- 条件法導入則
- 以下の前提が与えられているとき、pならばqである
- pであると仮定するとき、qである
- 以下の前提が与えられているとき、pならばqである
- 条件法除去則
- 以下の前提が与えられているとき、qである
- pである
- pならばqである
- 以下の前提が与えられているとき、qである
- 否定導入則
- 以下の前提が与えられているとき、pでない
- pであると仮定するとき、qかつ「qでない」
- 以下の前提が与えられているとき、pでない
- 否定除去則
- 『「pでない」でない』ならば、pである
ちなみに、この証明はかなり煩雑なので、読んでいるだけでは頭に入らないと思います。紙とペンを用意して、自分でも証明に挑戦してみてください。
- 「pである」と「pならばqである」を仮定する
- ①の2つの仮定に対して条件法除去則を使うと「qである」が導出される
- ②の導出結果に対して選言導入則を使うと「『pでない』またはqである」が導出される
- 「『「pでない」またはqである』でない」を仮定する
- ③の導出結果と④の仮定に対して連言導入則を使うと「『「pでない」またはqである』かつ『「『pでない』またはqである」でない』」が導出される
- ①で仮定した「pである」、及び⑤の導出結果に対して否定導入則を使うと、「pでない」が導出される
- ⑥の導出結果に対して選言導入則を使うと、「『pでない』またはqである」が導出される
- 「『「pでない」またはqである』でない」を仮定する
- ⑦の導出結果、及び⑧の仮定に対して連言導入則を使うと、「『「pでない」またはqである』かつ『「pでない」またはqである』でない』」が導出される
- ⑧の仮定、及び⑨の導出結果に対して否定導入則を使うと、『「『pでない』またはqである」でない』でない」が導出される
- ⑩の導出結果に対して否定除去則を使うと、「『pでない』またはqである」が導出される
- ①で仮定した「pならばq」、及び11の導出結果に対して条件法導入則を使うと、「『pならばq』ならば『「pでない」またはq』」が導出される
用いる仮定はどこかで必ず解除する必要があるため、非常に煩雑な証明になっています。ですがこれでもまだ半分。次は「『「pでない」またはq』ならば『pならばq』」を証明しなければなりません。
「『pでない』またはq」ならば「pならばq」であることを証明
「『「pでない」またはq』ならば『pならばq』」の証明は割と面倒くさいので、ステップを3つに分けます。
- 反復律(re)「pならばpである」を証明する
- 推論規則としての矛盾律(contrad)「『pかつ「pでない」』ならばqである」を証明する
- reとcontradを用いて、「『「pでない」またはq』ならば『pならばq』」を証明する
反復律(re)・推論規則としての矛盾律(contrad)は「派生規則」と呼ばれ、しばしば証明なしに用いられます。公理ではありませんが、最も公理に近い規則と考えて問題ありません。
この記事の中では初登場なので、一度証明しておきましょう。
反復律(re)「pならばpである」は以下の手順で証明できます。
- 「pでない」を仮定する
- 前提である「pである」と①の仮定に対して、連言導入則を使うと、「pかつ『pでない』」を導出できる
- ②の導出結果、及び①での仮定に対して、否定導入則を使うと、「『pでない』でない」を導出できる
- ③の導出結果に対して否定除去則を使うと、「pである」を導出できる
次に、推論規則としての矛盾律(contrad)「『pかつ「pでない」』ならばqである」を証明します。
- 「qでない」を仮定する
- 前提「pかつ『pでない』」と①の仮定に対して、連言導入則を使うと、「『pかつ「pでない」』かつ『qでない』」を導出できる
- ②の導出結果に対して連言除去則を使うと、「pかつ『pでない』」を導出できる
- ③の導出結果、及び①の仮定に対して、否定導入則を使うと、「『qでない』でない」を導出できる
- ④の導出結果に対して否定除去則を使うと、「qである」を導出できる
以上、reとcontradが証明されました。この2つの派生規則を使って、「『「pでない」またはq』ならば『pならばq』」を証明します。
証明の手順は以下の通りです。
- 「pである」を仮定する
- 「pでない」と「qである」を仮定する
- ①の仮定と、②における「pでない」の仮定に対して、連言導入則を使うと、「pかつ『pでない』」を導出できる
- ③の導出結果に対してcontradを使うと、「qである」を導出できる
- ②の仮定に対してreを使うと、「qである」を導出できる
- 前提「『pでない』またはq」および、②の仮定からの④・⑤の導出結果に対して、選言除去則を使うと、「qである」を導出できる
- ①の仮定、および⑥の導出結果に対して、条件法導入則を使うと、「pならばqである」を導出できる
というわけで、「『「pでない」またはq』ならば『pならばq』」も証明できました。
いや〜長かったですね。ともあれこれで、「pならばq」と「『pでない』またはq」が同値であるとわかりました。
この同値性を使うと、条件法の命題を全て選言に言い換えることができます。「ならば」よりも「または」の方が、証明するときに何かと使い勝手が良いので、ぜひ積極的に言い換えてみてくださいね。
命題論理の証明②:空疎に真
最後に紹介するのは、意味論の難関「空疎に真」です。
空疎に真とは何かというと、「pならばq」という命題は、pが偽である場合必ず真になる、ということです。
真理値表では以下のように表現できます(赤線で囲った部分に注目してください)。
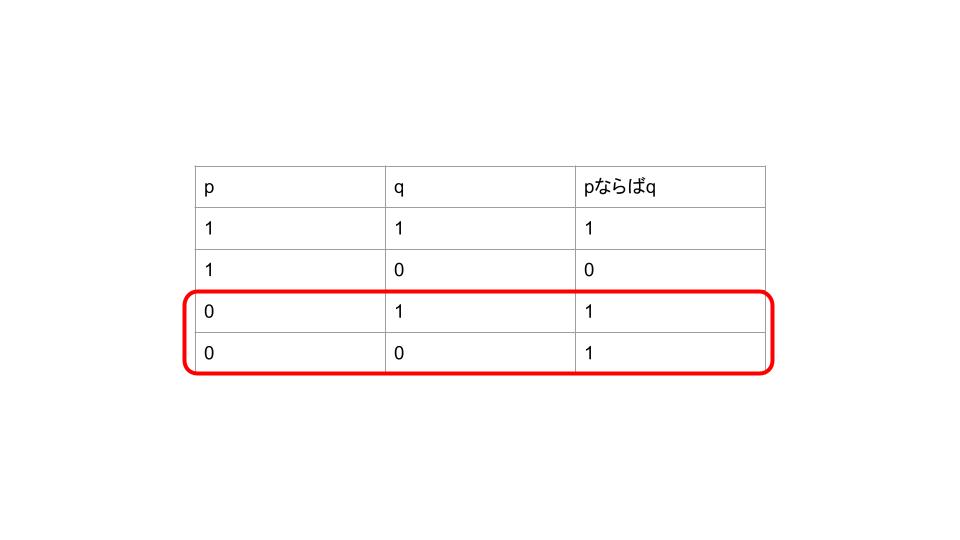
「pならばq」という命題が、「pでない」という条件の元で必ず真になる……というのは、直感的には信じ難いですよね。そこで、この「空疎に真」を構文論的に証明してみましょう。
「空疎に真」を構文論的に言い直すと、
「『pでない』ならば『pならばq』」
になります。
早速証明してみます。手順は以下の通りです。contradを使うので、「『「pでない」またはq』ならば『pならばq』」の証明も見ながらご覧ください。
- 「pである」を仮定する
- ①の仮定、および前提「pでない」に対して、連言導入則を使うと、「pかつ『pでない』」を導出できる
- ②の導出結果に対してcontradを使うと、「qである」を導出できる
- ①の仮定、および③の導出結果に対して、条件法導入則を使うと、「pならばq」を導出できる
意外とシンプルですね。
空疎に真の証明で肝になるのはcontradの部分です。「pかつ『pでない』ならばqである」というやつですね。前提が論理的に矛盾していれば、結論は何でもありになる。仮に結論となる命題それ自体が間違っているとしても、「前提→結論」という条件法の命題は常に真になる……。
なんとなく違和感がまだ残っている方もいるかもしれません。その感覚はおそらく正しく、この「空疎に真」が命題論理の大きな課題なのかもしれません。将来的には、この「空疎に真」がもっとわかりやすく証明される(あるいは、「空疎に真」が論理的に否定される)ようになれば良いなぁと個人的には思っています。
おわりに:命題論理のまとめ
いかがでしたか?
この記事では、命題論理の構文論・意味論について、かなり詳細かつ丁寧に解説してきました。
しかしおそらく、読んだだけでは今ひとつ腑に落ちない……と感じる人もいるでしょう。
そんな人は、ぜひ以下の書籍に掲載してある命題論理の練習問題を解いてみてください。数学と同じで、問題を解いているうちに、公理・定理の意味が徐々にわかるようになってくるはずです。
- 金子祐介『論理と分析——文系のための記号論理入門』、2019年、晃洋書房
- 金子祐介『文系のための記号論理入門——命題論理から不完全性定理まで』、2021年、朝倉書店
- 藤村龍雄『よくわかる記号論理』、2005年、勁草書房


